Student-Made Review Booklets

A very interesting idea was presented last week in our Grade 11 presentations. We were shown how to make little review booklets. These can serve as a quick reference material for the student, a study guide, perhaps even as a formula sheet for a test. I liked that this approach requires the students to make their own (as opposed to using a pre-made reference sheet). In grade 8, my history teacher had us make a table of contents in the front of our binders. We'd add to the table of contents as we took notes (and put page numbers on the top corners of our notes). This was a great lesson in organization and I see something similar in this. By this method, students have a short reference of everything they need to know, which may help their studying (since textbooks can be cumbersome sometimes). This would be a great method for physics as well, which has a lot of content and can be difficult to organize.

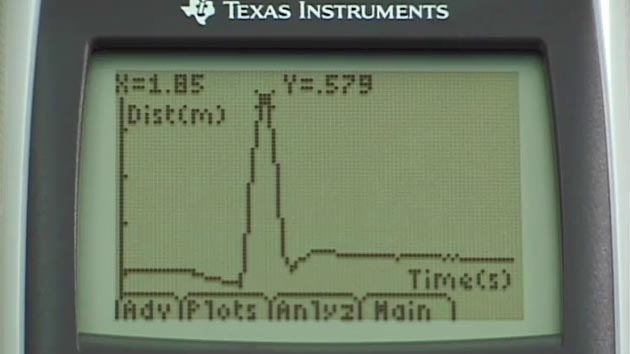
Generating Plots Using Motion Detectors

This week, an interesting application of TI graphing calculators was demonstrated. A calculator was connected to a motion detector which allowed a person walking in front of the detector to create a position-time graph. The exercise we were given was to recreate a given set of plots using the motion detector. It was a great way to connect slope with rate of change. The obvious physics applications didn't escape me. Kinematics, the unit that traditionally begins 11 Physics, requires developing an intuitive understanding of the position-time graphs. Students often have a difficult time relating what they see on the plot to a mental picture of actual motion. Curvature, as it relates to acceleration is particularly tricky. There is a difference between acceleration and "getting faster". Being able to create their own motion and seeing it plotted would be a very useful experience. Another difficulty students have is understanding that at turning points of a position-time curve, the speed is instantaneous zero, even though the acceleration is always non-zero. This would also be a useful exercise in calculus, when the topic of second derivatives come up.

 

Introducing the Concept of Proof to Students

This week we saw four more interesting miniature lessons. By a good coincidence, three of them dealt with mathematical proof to differing extents. I want to speak about one lesson in particular, which covered the following geometry problem:

https://static.guim.co.uk/sys-images/Guardian/Pix/pictures/2014/10/16/1413457021371/da4d4757-3177-4772-88e4-e481c7cdc8ee-bestSizeAvailable.gif

The object is to determine the sum of the three angles indicated in the figure. I believe this puzzle originated with Martin Gardner (an excellent source for clever math problems and riddles) but I am not positive. We were given Geoboards and elastic bands as tools to help solve the problem. In addition, we we cut up a copy of the figure in order to see that the three angles should sum to a right angle. Although it's a very good problem, this was a rather difficult exercise (perhaps due the fact that we weren't expecting it). It made me wonder how it would be received by grade 10 students. However, if they had been working up to this exercise over the term by doing simpler geometric proofs, perhaps it would not catch them as off-guard. It is probably easier in the beginning to learn proof by proving the obvious, so whether this problem is at-level would depend on how many similar exercises the class had already seen. It is definitely the type of thing that needs to be seen by students more often, and early. If I had a choice, I would have done an algebraic proof, but being forced to do a geometric proof showed me how bad I really am at that kind of thing.

My first real encounter with proof was a second year university algebra course and it completely revolutionized my impressions of mathematics. It was not difficult, it taught me to think, and I really wished that I had seen something like that earlier. Another benefit of proof, particularly of the geometric kind, is that is does not use numbers. It is a purely logical/visual expression of math which I imagine many students may find refreshing, particularly those whose numeracy may be lagging behind their peers. Does the prevalence of calculation, data, word problems etc. perhaps create an implicit bias in the students' minds with respect to what mathematics actually is? Even geometry, when it is taught, is less about structure and more about numerical quantities of area, volume and so on. Which is more fundamental after all, shape or quantity? In schools, quantity seems to be hands-down winner of that debate (whether the debate ever took place I do not know). Perhaps it may be that the math class could do with fewer numbers.

Story Based Math Problems and Proportional Reasoning

Last week in our math course, we saw presentations of three condensed lessons. The topics covered were finance, graph transformations, and calculating volumes. Although all were good, I was to focus on the “volumes” lesson for this post. Nam (the presenter) based his lesson on the film adaption of the book “Holes”, which is a very common presence in the junior school English class. For those who haven’t read it, Holes is a young adult novel about a boy named Stanley who is wrongly convicted of theft and sent to a sort of juvenile disciplinary camp where the inmates are forced to dig a hole every day out in the desert. The depth of the hole and the diameter must be equal to the length of the inmate’s shovel. Nam started the class with a clip from the movie in which Stanley accidently gets in trouble with another inmate for grabbing a shovel slightly shorter than the rest of them. The question Nam posed to the class is, “does it really matter if the shovel is a bit shorter”. He then had us try and figure out how much less dirt we would have to dig over the course of a year if we used the shorter shovel (it turned out to be about a month’s worth of holes). I liked this set up for a lesson because it starts with familiar territory. Practically everyone in the class had read Holes so when we worked on this problem, we already had a context in mind for the problem. I also liked that I was surprised by the answer, I didn’t expect the difference in volumes would be so significant. All in all, it showed me the effectiveness of using stories to engage students with a problem (as opposed to the more generic types of word problems we often encounter). If I had one thing to improve upon, it would be the organization of the problem. The problem was posed in feet and inches and we were made to convert everything to metric units. This made the problem a bit numbers heavy. Additionally, it was a bit ambiguous what was meant by “how fewer holes …” since we had two different volumes. This is nitpicky of course, and easy to fix. An alternate approach could be to do away with inches and metres altogether and use the standard shovel length as your unit length. For example, if the shorter shovel was 7/8 of the standard shovel, the smaller hole has (7/8)³ the volume of a standard hole. This greatly simplifies the calculation and may be a useful way of incorporating proportional reasoning.

Using Diagrams and Manipulatives to teach the Sine Law's "Ambiguous Case"

Looking over my blog and realizing that I neglected to reflect on our lesson on manipulatives, I thought I would use this post to discuss one particular application about which I have been thinking a great deal. I had my first real day in a school last week and I sat in on two math classes, one grade 9 and the other grade 11. In the grade 11 class (a fairly large one), the topic of the day was the Sine Law and the "ambiguous case". For those who may be a bit rusty, the ambiguous case refers to the situation where more than one triangle can be constructed from the information given (2 sides and an angle). Mathematically, the ambiguity can be seen from the fact that sin(x) is not one-to-one, where x ranges from 0 to 180 degrees. Some of the students in the class had difficulty grappling with the idea of there being more than one solution. Although I was mostly watching, bits of conversation I heard made me think that the deeper issue related to the qualities of sin(x) as a function. Although its not a term they would use, the students seemed to be assuming that sin(x) was bijective. I was trying to think of ways to discuss the Sine Law and the different cases (no solution, one solution, two solutions) as simply as possible. The diagram as I've often seen it drawn shows the fixed side and angle, with the two possible fixed-length sides superimposed.

I included the red line in order to emphasize that the triangle outlined by the green lines is an isosceles triangle. The difficulty with the above diagram is that although there are only two triangles of interest, there are six triangles that appear. This leads to confusion with respect to where we should be looking, and what each line represents. One diagram I prefer, though I can't find many examples of it online, is to build the three cases from the intersection of the two black lines show above with a circle.

Shown above are the same two black lines as before. Three different segments were chosen for the second fixed-length side. Imagine that these were rods rotating on an axis fixed at the upper vertex of the triangle, I traced out the circle that the free end of each rod would draw. The intersection of the horizontal black line with any given circle marks the position the rotating segment would have to make in order to complete the triangle. The blue circle never intercepts and so has no solution. The red circle touches the line tangentially at one point and so has one solution. The green circle has two intercepts and so has two solutions (the ambiguous case). I could have more thorough and drawn a fourth, larger circle that also has only one solution.

I like this diagram because it contains a lot of information yet presents it in what I feel is the simplest and most natural way. The fixed properties remain fixed and it is clear that the only variable is the orientation of the second side. Practically, this diagram could be made in a few ways. I would be drawn from scratch by a student using a compass and a rule. What's nice about this approach is that as the circles get larger and larger, the nature of the solutions changes. This would lead to a natural path of investigation through which the student can be guided into deriving expressions that define each of the four cases. More tangibly, the black lines could be drawn on a piece of construction paper with a marker. The length of the second side could be chosen and a compass could be used to find the orientation(s) of that side. Alternatively, the side could be made out of strip of construction paper and rotated by hand until a solution is found. In whatever approach is used, it would to a good demonstration of the Sine Law and the ambiguous case, as well as connection between calculation and measurement.

“forgottenbooks.com” as a Historical Teaching Resource

This week­ we looked at the idea of using games in order to teach mathematical concepts. It began with a round of “headbands”. Normally when this game is played, each player has a noun taped to their forehead and they play ’20 questions’ to try and figure out what it is. In this version, instead of a noun, we had a quadratic function. This was an interesting spin on the game. I don’t know how other people played, but for myself, I first figured out the form of the function (factored, vertex, expanded) and then guessed the parameters. I’m not sure how much could be learned from this game but it is certainly a good way to test your facility in mathematical vocabulary. For example, if I ask “is the function in vertex form”, does the student know that is actually saying “does the function look like f(x) = a(x-b)²+c”? We went from there to discuss different video games and apps that have been developed for the teaching of mathematics. I reserve a slight amount of skepticism with respect to how much can be absorbed passively from playing these games, but as a matter of practicing a concept, I imagine a student will get through many more practice problems if they are disguised as games (chocolate-covered broccoli, as Amy Lin put it). The side of technology that really intrigues me is its use as a virtual manipulative. For example, apps that allow for an intuitive visualization and manipulation of geometric figures would have a useful degree of flexibility that their tangible counterparts would not have.

Since we have a whole forum dedicated in this class to the discussion of different apps, I want to bring up a potentially useful but quite different type of resource.  There is an online PDF library called “Forgotten Books” which contains literally hundreds of thousands of rare historical books on every subject imaginable, from Renaissance literature to essays on witchcraft. Membership can be free or purchased (about $8 a month). The free membership gives unlimited access to all of the books, but every couple of pages the image will be blocked. The paid membership removes the barrier. I bring up this site because it contains many historical works on mathematics as well as math pedagogy. These books present a very interesting perspective and explain concepts in a way that may be unexpected and possibly useful to a teacher. They also make reference to different manipulatives that could be of interest to the modern reader. These are often simple, and could be made by hand without much difficulty. They would also make good projects for someone who would like to try 3D printing. These books can also serve as sources of interesting and instructive word problems as well as ideas for simple yet effective demonstrations of mathematical concepts.

Another use for this library is as a source for historical perspectives on mathematics and pedagogy. These books being so old (+100 years), I find this perspective very refreshing. At the same time, it is very interesting to read a textbook from more than a century ago and see that many of the concepts we credit to modern enlightenment such as “student-centered learning” (and even differentiated instruction, to a degree), were practices treated as merely common sense. In fact, the more I read these books, the more I feel that the derision “traditional” education faces these days is built on a straw man, but I digress. One part of the library I would particularly like to explore are the books on Jesuit education and their pedagogical philosophy. This is not something I know much about, but the historical importance of the Jesuits on the scientific revolution was first impressed upon me when I read Rene Descartes’ biography, Cogito Ergo Sum. In addition to training many of history’s most important mathematicians and physicists (including Descartes), they also educated Marin Mersenne, a French priest who single-handedly organized and maintained correspondence and collaboration between nearly 140 different mathematicians, philosophers, and scientists from all across Europe (a thankless task whose historical importance could not be understated). In conclusion, Forgotten Books is a very fun site to explore. The sheer variety of books available is such that you never know what you will find when you browse, but you will always find something worth reading.

Gradus ad Parnassum

In my previous post, I wrote briefly about a historically important pedagogical work in music theory entitled Gradus ad Parnassum, or in English, The Steps of Parnassus, (Parnassus being the mythical home of the Muses). This work first appeared in 1725 and has never fallen out of use, being used by composers and teachers ranging from Mozart to Brahms to Richard Strauss. The author was Joseph Fux, a major composer of the late Baroque period. Although his fame as a composer has not survived as well as some of his contemporaries, J.S Bach and Handel being obvious examples, he was highly admired in his own time and occupied during his career the most prestigious musical post in the world: Music Director of the Viennese Court. I would like to speak in more detail about the Gradus because I feel there is much that we can learn from Fux’s approach that can be applied to the teaching of mathematics and physics. It may be surprising to some that a parallel could be drawn between mathematics and music pedagogy, but the actual art of composition is more systematic that some would think. It is part art and part science, much like mathematics itself.

In any math problem of a particular level of sophistication, it is the general aim of the student to arrive at the correct answer.  In other words, there is some unknown value or function (in the case of a differential equation) and the object of the game is to derive an expression for the unknown. This is most systematic level of mathematics. For example, given a Hookean spring with particular characteristics attached to a mass with certain initial conditions, a differential equation can be written from which the motion of the spring can be obtained. Beyond obtaining that function, there is little that can be drawn from that problem. One step above in sophistication would be to study the problem more generally, studying the system while directly specifying as little as possible. This would enter the region of mathematical proof (as in, to prove that the period of a Hookean spring does not depend on the amplitude of the oscillation). It has been my experience that this kind of mathematics has something in it akin to art: we take certain facts and try to arrange them, or follow their implications in such a way that a whole new fundamental truth is revealed, not merely the specific truth or a particular system with particular values. In music it is somewhat similar, to arrange sounds and pitches in a new and meaningful way. The difference is that in mathematics, the aim is consistency, which is objective; in music, the aim is aesthetic appeal, which is partially subjective. Music theory is the system of rules and conventions that attempt to formalize ‘correctness’ in composition. Unlike in mathematics, these rules are not unbreakable but rather “for the guidance of the wise and the obedience of fools”. By this I mean that good composers break these rules when they desire a particular effect, while bad composers break them because they lack the skill to follow them.  Turning now to the Gradus ad Parnassum, Fux outlines his pedagogical philosophy in his introduction:

There have certainly been many authors famous for their teaching and competence, who have left and abundance of works on the theory of music; but on the practice of writing music they have said very little, and this little is not easily understood. Generally, they have been content to give a few examples, and never have they felt the need of inventing a simple method by which the novice can progress gradually, ascending step by step to attain mastery in this art. I shall not be deterred by the most ardent haters of school, nor by the corruptness of the times … Seeking a solution to this problem, I began, therefore, many years ago, to work out a method similar to that by which children learn first letters, then syllables, then combinations of syllables, and finally how to read and write. And it has not been in vain. When I used this method in teaching I observed that the pupils made amazing progress within a short time. So I thought I might render a service to the art if I published it for the benefit of young students, and shared with the musical world the experience of nearly thirty years, during which I served three emperors (in which I may in all modesty take pride).

The work itself is written as an ongoing dialogue between a pupil Josephus and the teacher Aloysius (representing the Renaissance master Giovanni Pierluigi da Palestrina). Aloysius begins with a review of consonances and dissonances (which he assumes the student to already know) and then proceeds to introduce the three kinds of motion: direct, contrary, and oblique. He concludes the introduction with the four fundamental rules of counterpoint:

1.     From one perfect consonance to another perfect consonance, one must proceed in contrary or oblique motion.

2.     From a perfect consonance to an imperfect consonance, one may proceed in any of the three motions.

3.     From an imperfect consonance to a perfect consonance, one must proceed in contrary or oblique motion.

4.     From one imperfect consonance to another imperfect consonance one may proceed in any of the three motions.

These rules form basically all the information that the reader (living vicariously through Josephus) needs for the first lesson. Aloysius presents the student with a melody (or cantus firmus) and has him harmonize it in simple note-on-note counterpoint. This is the musical equivalent to a simple word problem. The fictional student presents his answer and explains to the teacher how he arrived at it. However, the student’s answer is not perfect and Josephus corrects it. Some of the mistakes are from breaking one of the Four Rules. Some mistakes are subtler, such as not setting the counterpoint in the same mode as the cantus firmus.

When I read this example, I thought at the time that it seemed somewhat sloppy, throwing information at the student after the fact. However, speaking for myself, the phrase “set the counterpoint in the same mode as the cantus firmus” was easier for to understand from the mistaken example than from the rule itself. The student’s work then becomes an instructional example, with the teacher demonstrating what he could do to avoid the error. This is the general pattern of the book. Very small amounts of information are introduced at a time, which allows for a steady but never overwhelming increase in complexity. The work progresses while remaining in two-part harmony, through the first, second, and third species of counterpoint, ligatures, and florid counterpoint. Having exhausted this type of composition, Fux then goes back to the beginning and does it all over again in three-part and four-part harmony.

When I read this book, barely more than 100 pages, I wonder what specifically it is that made it so effective. What struck me first was how old fashioned the compositional style being taught was. The Baroque period was coming to a close at the time of writing. Renaissance polyphony, which had been essentially replaced with Baroque counterpoint, was quickly giving way to the Rococo style. What Fux was intending with this book was to solidify the old way of doing things, not because he felt that people ought to write that way, but because he saw that the young composers were ignorant of the historical foundations of their art and were becoming reckless and unbounded by any standards of taste. He says this explicitly in his introduction where he states that that his purposes “do not tend – nor do I credit myself with the strength – to stem the course of a torrent rushing precipitously beyond its bounds. I do not believe that I can call back composers from the unrestrained insanity of their writing to normal standards.” Music pedagogy then, was either too theoretical or heavy with information, or it was too undisciplined, prompting a great deal of activity yet resulting in an overall decline of quality and technical mastery.

I wonder sometimes if these two errors are still present to some extent in mathematics (and physics) pedagogy. I’m always struck when I tutor high school students what tomes their textbooks are, and how difficult it is to find what I’m looking for in them. This would be an example of too much information, particularly when the underlying concept is very simple. It frustrates me enormously whenever I work with a first-year university student, and find that after two years of high school physics they still can’t do any kind of projectile motion problem without flipping back and forth through the textbook, or define for me Newton’s 2^nd Law or the Work-Energy Theorem (and this happens a lot). The textbook almost functions for them as a book of spells instead of an instructional tool. The other extreme is when creativity and discovery is emphasized at the expense of formal instruction, in the expectation that students through exploration will spontaneously discover the principles they need. (Re, “We Don’t Want No Education” by Theodore Dalrymple). I expect that in some circumstances this may work very well, but I wonder at the same time if it can allow serious misconceptions slip past the teacher. Also, I wonder if making a subject appear more subjective that it really is can inadvertently encourage in students a relativist epistemology. Whatever the virtues of the present age, I don’t believe due respect to Principle of Non-Contradiction is one of them.

I believe that part of the brilliance of Fux’s text is the skill with which he takes the middle road. In modern parlance, it is very ‘student-centered’ in that the student in the dialogue does the bulk of the work, and information is introduced very gradually. There is no deluge of information but rather, knowledge of music theory is grown naturally in the student through the use of exercises. At the same time, Fux does not beat about the bush with respect to the student’s ignorance of the subject. He presents his rules and methods as law and not as a matter of debate. He sometimes explains his rationale to the student and sometimes refuses to, if he feels the explanation is premature or would confuse the student more. At one humorous point in the dialogue, Aloysius advises Josephus not to get over-confident and to remember his place:

I want to remind you again and again to make every effort to overcome the great difficulties of the study you have undertaken; and neither to become discouraged by hard work; not to allow yourself to be deterred from unflagging industry by flattery of such skill as you have already achieved. If you will work thus you will be delighted to see the way in which light gradually illuminates had been obscure and how in some manner the curtain of darkness seems to be drawn away.

To conclude, part of me wonders what a math or physics instruction book would look like written in this manner, and if it would even be possible. Being a dialogue, it is not particularly useful as a reference, but I think this format makes it especially effective as an instruction tool. It is possible to read a textbook and come away thinking that you’ve learned something: perhaps you have, and perhaps you haven’t. However, it would be just about impossible to read Gradus ad Parnassum and convince yourself that you’ve learned something if you haven’t also done the exercises. Yet history shows us that someone who diligently works his way through the entire book could gain an enormous amount of skill and understanding. As such, Fux’s work is not so much a textbook in the modern sense but an actual pedagogical program. I won’t speculate on how effectively this method could be transplanted from music theory to mathematics, but as someone who has had to learn both, the natural similarities between these two subjects make me believe that anyone who wants to learn how to present mathematics in an intuitive guise and a sensible order may glean many useful ideas from this work.