Student-Made Review Booklets

A very interesting idea was presented last week in our Grade 11 presentations. We were shown how to make little review booklets. These can serve as a quick reference material for the student, a study guide, perhaps even as a formula sheet for a test. I liked that this approach requires the students to make their own (as opposed to using a pre-made reference sheet). In grade 8, my history teacher had us make a table of contents in the front of our binders. We'd add to the table of contents as we took notes (and put page numbers on the top corners of our notes). This was a great lesson in organization and I see something similar in this. By this method, students have a short reference of everything they need to know, which may help their studying (since textbooks can be cumbersome sometimes). This would be a great method for physics as well, which has a lot of content and can be difficult to organize.

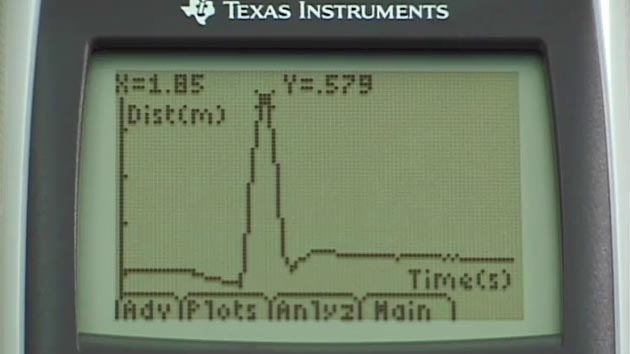
Generating Plots Using Motion Detectors

This week, an interesting application of TI graphing calculators was demonstrated. A calculator was connected to a motion detector which allowed a person walking in front of the detector to create a position-time graph. The exercise we were given was to recreate a given set of plots using the motion detector. It was a great way to connect slope with rate of change. The obvious physics applications didn't escape me. Kinematics, the unit that traditionally begins 11 Physics, requires developing an intuitive understanding of the position-time graphs. Students often have a difficult time relating what they see on the plot to a mental picture of actual motion. Curvature, as it relates to acceleration is particularly tricky. There is a difference between acceleration and "getting faster". Being able to create their own motion and seeing it plotted would be a very useful experience. Another difficulty students have is understanding that at turning points of a position-time curve, the speed is instantaneous zero, even though the acceleration is always non-zero. This would also be a useful exercise in calculus, when the topic of second derivatives come up.